| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
- Convolutional Neural Network
- backpropagation
- 합성곱 신경망
- Python
- A Neural Algorithm of Artistic Style
- 역전파법
- bayesian
- 오일러 프로젝트
- SQL
- 역전파
- 딥러닝
- CNN
- 비샤몬당
- 전처리
- 오토인코더
- 베이지안
- deep learning
- neural network
- 히토요시
- mnist
- 소수
- project euler
- Gram matrix
- 냥코 센세
- 자전거 여행
- Autoencoder
- c#
- 소인수분해
- 신경망
- 수달
- Today
- Total
목록neural network (11)
통계, IT, AI
 딥러닝: 화풍을 모방하기 (13) - 논문 구현
딥러닝: 화풍을 모방하기 (13) - 논문 구현
1. 개요 A Neural Algorithm of Artistic Style은 2015년에 발표된 논문으로, 신경망을 이용하여 특정 이미지를 다른 이미지의 화풍을 모방하여 재구성하는 내용을 담고 있다. 발표가 된 직후부터 상당히 화제가 된 논문으로 내가 신경망에 관심을 갖게 된 계기이기도 하다. 본 포스팅에서는 해당 논문에서 소개한 style transfer의 원리를 간략하게 설명하고 논문에 등장한 figure를 재현한다. 2. 원리와 재연 본 논문에서 제시하고 있는 방법은 한 이미지에서는 내용을, 다른 이미지에서는 스타일을 학습하고 결과를 적절하게 혼합하여 이미지를 생성하는 것이다. 먼저 내용을 학습하는 방법을 설명한다. Convolution layer는 filter를 통해 이미지의 특징을 잡아내는 역..
 딥러닝: 화풍을 모방하기 (10) - 연습: 자기부호화기(Autoencoder)
딥러닝: 화풍을 모방하기 (10) - 연습: 자기부호화기(Autoencoder)
1. 개요 Autoenoder를 실습하기 위하여 두가지 주제를 진행하였다. 첫번째는 의 그림 5-6을 재연하는 것이고 두번째는 Autoencoder로 사전학습을 하여 신경망의 학습이 잘 이루어지는지 확인하는 것이다. 즉, 신경망의 층이 많아지면 학습이 잘 이루어지지 않는 현상인 Gradient vanishing을 Autoencoder로 해결할 수 있는지 알아보고자 하였다. 재연을 위한 모든 코드는 깃허브의 deeplearning 폴더에 올려두었다. 실행을 위해서는 data/mnist 폴더의 mnist_loader.py를 실행하여 pkl 파일을 생성해야 한다. 2. 그림 5-6 재연 의 그림 5-6은 자기부호화기의 파라미터가 시각적으로 어떠한 경향을 갖는지 표현한 것으로 아래 그림 1과 같다. 입력층의 노..
 딥러닝: 화풍을 모방하기 (9) - 책 요약: 5. 자기부호화기
딥러닝: 화풍을 모방하기 (9) - 책 요약: 5. 자기부호화기
5. 자기부호화기: Autoencoder5.1. 개요 자기부호화기(Autoencoder)란 출력이 입력과 같도록 설계한 신경망이다. 예를 들어 그림 5-1과 같이 입력층과 출력층의 유닛의 수가 서로 같은 2층의 신경망을 생각해보자. 1층에서는 입력 \(x\)가 \(f(Wx+b)\)를 거쳐 \(y(x)\)로 부호화된다. 2층에서는 \(y(x)\)가 \(\tilde{f}(\tilde{W}y(x)+\tilde{b})\)을 통하여 \(x\)로 복호화된다. 즉, 이 신경망의 목표는 입력을 부호화한 뒤 이어 다시 복호화했을 때 원래의 입력을 충실하게 재현할 수 있는 파라미터를 찾는 것이다. 5.2. 자기부호화기의 설계 5.2.1 출력층의 활성화 함수와 오차함수 자기부호화기의 활성화 함수는 중간층의 \(f\)와 출력..
 딥러닝: 화풍을 모방하기 (7) - 책 요약: 4. 역전파법
딥러닝: 화풍을 모방하기 (7) - 책 요약: 4. 역전파법
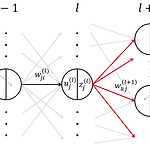
4. 역전파법: backpropagation 4.1 기울기 계산의 어려움 - 3장에서 설명한 경사하강법을 실행하기 위해서는 식 \((1)\)과 같이 \(E_n(\boldsymbol{w})\)에 대한 미분이 필요하다. 단, \(w^{(l),t}_{ji}\)는 \(t\)시점의 파라미터를 나타내며 \(E_n(\boldsymbol{w})\)은 \(n\)번째 미니배치의 오차함수이다. $$ w^{(l),t+1}_{ji} \leftarrow w^{(l),t}_{ji} - \epsilon \frac{\partial E_n(\boldsymbol{w})}{\partial w^{(l)}_{ji}} \tag{1}\label{(1)}$$ - 그런데 이 미분을 계산하는 것은 입력에 가까운 층일 수록 힘들다. 왜냐하면 \(\bol..
 딥러닝: 화풍을 모방하기 (6) - 연습: 다클래스 분류 문제
딥러닝: 화풍을 모방하기 (6) - 연습: 다클래스 분류 문제
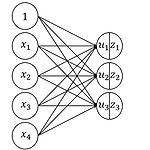
1. 개요- 입력이 4개이며 출력은 3가지 클래스를 갖는 경우를 생각해보자. 신경망은 그림 1과 같다.- 입력과 파라미터를 아래와 같이 정의한다.$$\begin{eqnarray} x_n&=& \begin{bmatrix}x_{n1} & x_{n2} & x_{n3}& x_{n4} \end{bmatrix}, \quad w=\begin{bmatrix}w_{11} & w_{21} & w_{31} \\ w_{12} & w_{22} & w_{32} \\ w_{13} & w_{23} & w_{33} \\ w_{14} & w_{24} & w_{34} \end{bmatrix}, \quad b=\begin{bmatrix}b_{1} & b_{2} & b_{3} \end{bmatrix} \\ \\ u&=&\begin{bmatr..
 딥러닝: 화풍을 모방하기 (5) - 연습: 이진 분류 문제
딥러닝: 화풍을 모방하기 (5) - 연습: 이진 분류 문제
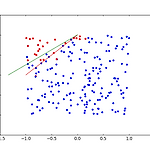
1. 개요- 변수가 2개이며 종속변수가 이진형인 경우를 생각해보자. 신경망은 그림 1과 같다.- 훈련데이터의 수는 200으로 한다. - 출력이 이진형이므로 활성함수는 sigmoid로 한다. - 즉, \(u_1=w_{11}x_1+w_{12}x_2+b_1\)이며 \(z_1=f(u_1)=1/(1+exp(-u_1))\)이다. - \(x_1\)과 \(x_2\)는 \(U(-1,1)\)에서 각각 독립적으로 생성한다.- 출력 \(d\)는 아래와 같이 정의한다. 단, \(\varepsilon\)은 \(N(0, 0.3^2)\)를 따른다.\begin{eqnarray}d = \begin{cases} 1 & \text{if } x_2 > x_1 + 1 + \varepsilon \\ 0 & \text{otherwise} \end..
 딥러닝: 화풍을 모방하기 (4) - 연습: 회귀 문제
딥러닝: 화풍을 모방하기 (4) - 연습: 회귀 문제
1. 개요- 다음 파트로 넘어가기 전에 지금까지 배운 것을 구현하여 이해를 확실하게 하자. - 가장 간단한 경우부터 연습하기 위하여 변수가 1개인 회귀 문제를 선택한다. 즉, 신경망은 다음과 같다. - 출력층의 활성함수는 항등함수로 한다. 그러므로 \(u_1=w_{11}x_1+b_1\)이며 \(z_1=f(u_1)=u_1\)이다. - 연습에 사용할 \(x_1\)은 \(U(-4,4)\)에서 200개를 생성한다. - 출력 \(d\)는 \(x_1-1+\varepsilon\)이며 \(\varepsilon\)은 \(N(0,1)\)를 따른다. - 데이터의 형태는 그림 2와 같다. 붉은 선은 연습에서 추정해야 할 파라미터를 나타낸다.- minibatch를 사용하며 1개의 batch size는 20으로 하며 반복횟수(e..
 딥러닝: 화풍을 모방하기 (3) - 책 요약: 3. 확률적 경사 하강법
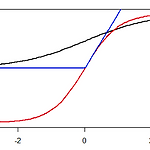
딥러닝: 화풍을 모방하기 (3) - 책 요약: 3. 확률적 경사 하강법
3. 확률적 경사 하강법: Stochastic Gradient Descent 3.1 경사 하강법 - 학습의 목표는 \(\boldsymbol{w}=\underset{\boldsymbol{w}}{argmin}E(\boldsymbol{w})\)을 찾는 것이다. 그런데 \(E(\boldsymbol{w})\)가 일반적으로 볼록함수가 아니기 때문에 전역 극소점을 찾는 것이 매우 어렵다. 하지만 어떤 국소 극소점에서의 \(E(\boldsymbol{w})\)가 충분히 작다면 문제를 해결할 수 있다. - 이러한 점을 찾는 방법에는 경사 하강법이 있다. - 먼저 다음과 같이 \(E\)의 기울기를 구한다. 단, \(M\)은 \(\boldsymbol{w}\)의 성분 수이다. $$\nabla E(\boldsymbol{w})=\..
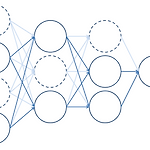
 딥러닝: 화풍을 모방하기 (2) - 책 요약: 2. 앞먹임 신경망
딥러닝: 화풍을 모방하기 (2) - 책 요약: 2. 앞먹임 신경망
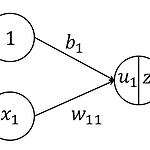
2. 앞먹임 신경망: Feedforward Neural Network 2.1 유닛의 출력 - 앞먹임 신경망은 층(layer) 모양으로 늘어선 유닛이 인접한 층과 결합한 구조이다. - 정보가 입력 측에서 출력 측으로만 흐르기 때문에 Feedforward라는 이름이 붙여졌다. - Multi-layer perceptron이라고도 부르지만 최초 제안된 perceptron은 입출력 함수가 step 함수로만 제한되었기 때문에 약간 다르다.- 유닛 한 개의 입출력의 예시는 아래와 같다. - 이 유닛이 받는 총 입력은 \(u_1=b_1+w_{11}x_1+w_{12}x_2+w_{13}x_3+w_{14}x_4\)이다.- \(b_1\)은 bias라고 부르며 1에 곱해지는 가중치이다.- \(w_{ji}\)는 입력에 대한 가중..
1. 시작하며 1.1 신경망 연구의 역사 1.1.1 다층 신경망에 대한 기대와 실망 - backpropagation의 등장하면서 신경망 연구에 진전이 있었으나 아래의 두가지 이유 때문에 붐이 끝나게 되었다.- 첫째, backpropagation은 다층 신경망에서의 overfitting을 막을 수 없었다. - 둘째, 이론을 만들기 어려워 연구가 어려웠다.- 단, Convolutional Neural Network; CNN은 다층 신경망에서 학습에 성공했고 특히 이미지 인식에서 좋은 성능을 보였으나, 신경망 연구에 대한 관심이 떨어지면서 CNN 또한 그렇게 되었다. 1.1.2 다층 신경망의 사전훈련(pre-training) - 다층 신경망에 대한 사전훈련을 통하여 학습이 원활하게 이루어짐이 보고됨에 따라 신..
