| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 역전파법
- deep learning
- Python
- 역전파
- 전처리
- 소수
- CNN
- 수달
- 합성곱 신경망
- 딥러닝
- neural network
- 비샤몬당
- bayesian
- c#
- 베이지안
- Convolutional Neural Network
- backpropagation
- Gram matrix
- 히토요시
- 냥코 센세
- 오일러 프로젝트
- 소인수분해
- A Neural Algorithm of Artistic Style
- 자전거 여행
- project euler
- 오토인코더
- Autoencoder
- 신경망
- SQL
- mnist
- Today
- Total
목록분류 전체보기 (94)
통계, IT, AI
 딥러닝: 화풍을 모방하기 (9) - 책 요약: 5. 자기부호화기
딥러닝: 화풍을 모방하기 (9) - 책 요약: 5. 자기부호화기
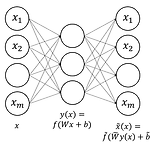
5. 자기부호화기: Autoencoder5.1. 개요 자기부호화기(Autoencoder)란 출력이 입력과 같도록 설계한 신경망이다. 예를 들어 그림 5-1과 같이 입력층과 출력층의 유닛의 수가 서로 같은 2층의 신경망을 생각해보자. 1층에서는 입력 \(x\)가 \(f(Wx+b)\)를 거쳐 \(y(x)\)로 부호화된다. 2층에서는 \(y(x)\)가 \(\tilde{f}(\tilde{W}y(x)+\tilde{b})\)을 통하여 \(x\)로 복호화된다. 즉, 이 신경망의 목표는 입력을 부호화한 뒤 이어 다시 복호화했을 때 원래의 입력을 충실하게 재현할 수 있는 파라미터를 찾는 것이다. 5.2. 자기부호화기의 설계 5.2.1 출력층의 활성화 함수와 오차함수 자기부호화기의 활성화 함수는 중간층의 \(f\)와 출력..
1. 개요 문제는 이곳에서 확인할 수 있다. 어떤 문자나 숫자의 역순이 원래의 것과 같다면 그 문자나 숫자를 palindrome이라고 한다. 585는 특이한 성질을 지니고 있는데 585와 그것의 2진수가 모두 palindrome이기 때문이다. 이와 같은 성질을 지닌 1,000,000 이하의 숫자의 합을 구하는 것이 문제의 목표이다. 2. 구현 어떤 수의 palindrome을 구하는 방법에는 여러가지가 있는데, 여기서는 나눗셈을 이용한 방법을 사용한다. 예를 들어, 115를 10으로 나누면 11의 몫과 5의 나머지가 나온다. 5에 10을 곱하여 이를 결과라고 하자. 11을 10으로 나누면 몫 1과 나머지 1이 나온다. 앞서 구한 결과에 10을 곱한 후 나머지 1에 10을 곱하여 결과에 더한 후 몫 1을 거..
1. 개요 문제는 이곳에서 확인할 수 있다. 197은 특이한 소수인데, 각 자리의 수를 순환시켜도 모두 소수이기 때문이다. 즉, 971, 719 모두 소수이다. 이와 같은 특성을 보이는 1,000,000 보다 작은 소수의 개수를 구하는 것이 목표이다. 단, 중복을 허용한다. 즉, 197, 971 그리고 719는 한가지 소수를 순환하여 만들 수 있지만 따로 센다. 2. 구현 ver 1.0 먼저 100만 이하의 소수를 에라스토테네스의 체를 이용하여 구한다. 이후 각 소수를 순환시키면서 그 수가 소수인지 확인한다. # -*- coding: utf-8 -*- import math as m # 1. Find primes lim = 1000001 prime_candidate = list(range(2, lim)) ..
1. 개요문제는 이곳에서 확인할 수 있다. 어떤 수는 각 자리의 factorial의 합으로 나타낼 수 있다. 예를 들면, \(145\)는 \(1!+4!+5!\)와 같다. 이러한 특징을 갖는 모든 수의 합을 구하는 것이 목표이다. 2. 구현 문제에 조건에 의하여 검사해야 할 숫자에는 상한선이 있다. 즉, \(n\)자리 숫자 중 가장 작은 수인 \(10^{n-1}\)이 \(n\)자리 숫자로 만들 수 있는 가장 큰 값인 \(9!n\)보다 작은 경우만 검사하면 된다. # -*- coding: utf-8 -*- import math as m n = 1 fact_9 = m.factorial(9) while 10**(n-1) < fact_9*n: n += 1 answer = 0 for i in range(10, fa..
보호되어 있는 글입니다.
 딥러닝: 화풍을 모방하기 (8) - 연습: 역전파법
딥러닝: 화풍을 모방하기 (8) - 연습: 역전파법
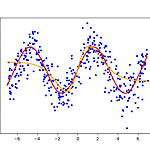
1. 회귀문제- 본 포스팅에 있는 결과는 다음 첨부파일(code.7z)을 통하여 재현이 가능하다.- 역전파법을 회귀문제에 적용해보자. 실습을 위해 정의역이 \((-7,7)\)인 구간에서, \(\sin\)함수에 정규분포를 따르는 오차를 주어 적합해보자. 은닉층이 없는 경우와 있는 경우도 비교해본다. \(\epsilon\)과 같은 하이퍼 파라미터에 대한 설정은 첨부된 압축파일의 main_sin.py에 있다. - 그림 1은 은닉층을 추가하지 않고 적합한 결과이다. 붉은 선은 \(\sin\)함수, 파란 점은 에러를 추가한 자료 그리고 주황 선이 적합한 결과이다. 출력층의 활성화함수가 항등함수이기 때문에 단순선형회귀의 결과와 같다. - 그림 2는 같은 자료에 1개의 은닉층을 추가한 결과이다. 은닉층의 노드의 수는..
1. 개요문제는 이곳에서 확인할 수 있다. \(49/98\)은 흥미로운 분수인데, 분자와 분모에 포함된 같은 수 9를 지우면 본래의 값과 같기 때문이다. 이와 같은 특성을 보이는 분수를 찾아 곱하고 약분한 후 분모의 값을 구하는 것이 목표이다. 단, 분자와 분모가 각각 두자리 수여야 하며 분수는 1보다 작아야 한다. 그리고 공통된 수는 0이 아니어야 한다. 이러한 특성을 보이는 분수는 4개가 있다고 한다. 2. 구현십의 자리가 \(a\), 일의 자리가 \(b\)인 어떤 두자리 수를 간략하게 \(ab\)로 나타내자. 분자와 분모에 공통적으로 포함된 같은 수를 \(d\)라고 하면 확인해야 할 분수의 형태는 \(da/db\), \(ad/db\), \(da/bd\), \(ad/bd\)의 4가지 밖에 없다. 또한..
1. 개요 문제는 이곳에서 확인할 수 있다. 7254는 39와 186의 곱으로 나타낼 수 있다. 즉 \(39 \times 186=7254\)이다. 이 수식에는 1부터 9까지의 숫자가 한번씩만 사용되었다. 7254와 같이, 1부터 9까지의 숫자를 한번씩만 사용하여 곱의 형태로 나타낼 수 있는 모든 숫자의 합을 구하는 것이 목표이다. 2. 구현 문제의 조건에 맞는 곱의 형태는 두가지 밖에 없다. 즉, 한자리 숫자와 네자리 숫자를 곱하여 네자리 숫자를 만드는 것과 두자리 숫자와 세자리 숫자를 곱하여 네자리 숫자를 만드는 경우 이외에는 문제의 조건에 맞지 않는다. 이를 이용하여 답을 구하자. # -*- coding: utf-8 -*- answer = [] # CASE 1: 1-digit multiply 4-di..
 딥러닝: 화풍을 모방하기 (7) - 책 요약: 4. 역전파법
딥러닝: 화풍을 모방하기 (7) - 책 요약: 4. 역전파법
4. 역전파법: backpropagation 4.1 기울기 계산의 어려움 - 3장에서 설명한 경사하강법을 실행하기 위해서는 식 \((1)\)과 같이 \(E_n(\boldsymbol{w})\)에 대한 미분이 필요하다. 단, \(w^{(l),t}_{ji}\)는 \(t\)시점의 파라미터를 나타내며 \(E_n(\boldsymbol{w})\)은 \(n\)번째 미니배치의 오차함수이다. $$ w^{(l),t+1}_{ji} \leftarrow w^{(l),t}_{ji} - \epsilon \frac{\partial E_n(\boldsymbol{w})}{\partial w^{(l)}_{ji}} \tag{1}\label{(1)}$$ - 그런데 이 미분을 계산하는 것은 입력에 가까운 층일 수록 힘들다. 왜냐하면 \(\bol..
1. 개요문제는 이곳에서 확인할 수 있다. 1, 2, 5, 10, 20, 50, 100 그리고 200을 사용하여 200을 만드는 방법의 수를 구하는 것이 목표이다. 이 문제는 재귀함수를 사용하여 간단하게 해결할 수 있다. 즉, 200에서 100을 빼고 나면, 문제는 100을 만드는 방법의 수를 구하는 것으로 변한다. 2. 구현: ver 1.0재귀함수를 이용하여 구현한다. 하지만 이 방법은 그다지 효율적이진 않은데, 만약 200이 아니라 400을 구하라고 해도 생각보다 시간이 오래 걸린다. 사람들의 아이디어를 참고하여 memoization을 사용하려고 했지만 아둔하기 짝이 없어 결국 이해하지 못했다. # -*- coding: utf-8 -*- import numpy as np coins = [200, 10..
