통계, IT, AI

1. 개요 A Neural Algorithm of Artistic Style은 2015년에 발표된 논문으로, 신경망을 이용하여 특정 이미지를 다른 이미지의 화풍을 모방하여 재구성하는 내용을 담고 있다. 발표가 된 직후부터 상당히 화제가 된 논문으로 내가 신경망에 관심을 갖게 된 계기이기도 하다. 본 포스팅에서는 해당 논문에서 소개한 style transfer의 원리를 간략하게 설명하고 논문에 등장한 figure를 재현한다. 2. 원리와 재연 본 논문에서 제시하고 있는 방법은 한 이미지에서는 내용을, 다른 이미지에서는 스타일을 학습하고 결과를 적절하게 혼합하여 이미지를 생성하는 것이다. 먼저 내용을 학습하는 방법을 설명한다. Convolution layer는 filter를 통해 이미지의 특징을 잡아내는 역..

1. 개요 CNN으로 Mnist 데이터를 학습해보자. 먼저 대략적인 구조는 그림 과 같다. 입력 데이터의 사이즈는 \((1,28,28)\)이다. 흑백 이미지이기 때문에 1개 채널이며 가로, 세로로 28 픽셀이다. 각 원소를 0부터 255사이의 값을 가지는데 이를 정규화하여 0부터 1사이의 값을 갖도록 변환한다. 합성곱층Convolution Layer에서 필터는 \((30, 5, 5)\)의 사이즈를 갖도록 한다. 따라서 합성곱층의 결과 데이터의 사이즈는 \((30, 24, 24)\)가 된다. 풀링층Pooling Layer은 최대 풀링Max Pooling을 사용하며 \((2,2)\)의 윈도우를 갖도록 한다. 따라서 풀링층의 결과 데이터는 \((30,12,12)\)의 사이즈를 갖는다. 풀링층의 결과 데이터는 ..

1. 개요 CNN(Convoluional Neural Network; 합성곱 신경망)은 특히 이미지 인식 분야에서 자주 사용되는 신경망이다. 지금까지 본 신경망(이하 완전연결 신경망)과 다른 점은 그림 과 같이 합성곱층(Convolution Layer)와 풀링층(Pooling Layer)이 추가되었다는 점이다. 2. 합성곱 계층 Convolution Layer2.1. 개요 완전연결 신경망이 가진 가장 큰 문제점은 데이터의 형상이 무시된다는 것이다. 예를 들어 MNIST와 같은 이미지 데이터에서는 픽셀들이 서로 밀접한 관련을 갖고 있다. 가령 1이라는 이미지는 아래 또는 위 방향으로 비슷한 픽셀 값을 가질 확률이 높다. 게다가 컬러 이미지는 채널까지 포함하여 3차원 데이터이지만 완전연결 신경망에서는 이러한..

1. 개요 나이브 베이즈는 베이즈 정리를 사용하는 확률 분류기의 일종으로 특성들 사이에 독립을 가정한다. 이론이 어렵지 않고 구현이 간단하며 "나이브"한 가정에도 불구하고 여러 복잡한 상황에서 잘 작동하기 때문에 다양한 분야에서 사용되고 있다. 독립변수에 따라 여러가지 모습을 가지지만 이번 포스팅에서는 어떤 메시지가 스팸(spam)인지 또는 정상(ham)인지 분류하는 문제만 고려한다. 2장에서는 나이브 베이즈 분류를 이해하기 위한 배경 지식을 간단하게 훑어보고 3장에서 나이브 베이즈가 어떤 식으로 작동하는지 살펴본다. 4장에서는 나이브 베이즈를 실제 데이터에 적용하여 텍스트 메시지를 분류해본다. 2. 배경 지식 2.1. 베이지안 통계 베이지안 통계에서는 모수 \(\theta\)가 고정된 값을 가지지 않고..

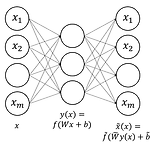
1. 개요 Autoenoder를 실습하기 위하여 두가지 주제를 진행하였다. 첫번째는 의 그림 5-6을 재연하는 것이고 두번째는 Autoencoder로 사전학습을 하여 신경망의 학습이 잘 이루어지는지 확인하는 것이다. 즉, 신경망의 층이 많아지면 학습이 잘 이루어지지 않는 현상인 Gradient vanishing을 Autoencoder로 해결할 수 있는지 알아보고자 하였다. 재연을 위한 모든 코드는 깃허브의 deeplearning 폴더에 올려두었다. 실행을 위해서는 data/mnist 폴더의 mnist_loader.py를 실행하여 pkl 파일을 생성해야 한다. 2. 그림 5-6 재연 의 그림 5-6은 자기부호화기의 파라미터가 시각적으로 어떠한 경향을 갖는지 표현한 것으로 아래 그림 1과 같다. 입력층의 노..

5. 자기부호화기: Autoencoder5.1. 개요 자기부호화기(Autoencoder)란 출력이 입력과 같도록 설계한 신경망이다. 예를 들어 그림 5-1과 같이 입력층과 출력층의 유닛의 수가 서로 같은 2층의 신경망을 생각해보자. 1층에서는 입력 \(x\)가 \(f(Wx+b)\)를 거쳐 \(y(x)\)로 부호화된다. 2층에서는 \(y(x)\)가 \(\tilde{f}(\tilde{W}y(x)+\tilde{b})\)을 통하여 \(x\)로 복호화된다. 즉, 이 신경망의 목표는 입력을 부호화한 뒤 이어 다시 복호화했을 때 원래의 입력을 충실하게 재현할 수 있는 파라미터를 찾는 것이다. 5.2. 자기부호화기의 설계 5.2.1 출력층의 활성화 함수와 오차함수 자기부호화기의 활성화 함수는 중간층의 \(f\)와 출력..

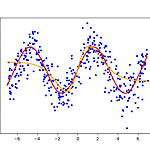
1. 회귀문제- 본 포스팅에 있는 결과는 다음 첨부파일(code.7z)을 통하여 재현이 가능하다.- 역전파법을 회귀문제에 적용해보자. 실습을 위해 정의역이 \((-7,7)\)인 구간에서, \(\sin\)함수에 정규분포를 따르는 오차를 주어 적합해보자. 은닉층이 없는 경우와 있는 경우도 비교해본다. \(\epsilon\)과 같은 하이퍼 파라미터에 대한 설정은 첨부된 압축파일의 main_sin.py에 있다. - 그림 1은 은닉층을 추가하지 않고 적합한 결과이다. 붉은 선은 \(\sin\)함수, 파란 점은 에러를 추가한 자료 그리고 주황 선이 적합한 결과이다. 출력층의 활성화함수가 항등함수이기 때문에 단순선형회귀의 결과와 같다. - 그림 2는 같은 자료에 1개의 은닉층을 추가한 결과이다. 은닉층의 노드의 수는..

4. 역전파법: backpropagation 4.1 기울기 계산의 어려움 - 3장에서 설명한 경사하강법을 실행하기 위해서는 식 \((1)\)과 같이 \(E_n(\boldsymbol{w})\)에 대한 미분이 필요하다. 단, \(w^{(l),t}_{ji}\)는 \(t\)시점의 파라미터를 나타내며 \(E_n(\boldsymbol{w})\)은 \(n\)번째 미니배치의 오차함수이다. $$ w^{(l),t+1}_{ji} \leftarrow w^{(l),t}_{ji} - \epsilon \frac{\partial E_n(\boldsymbol{w})}{\partial w^{(l)}_{ji}} \tag{1}\label{(1)}$$ - 그런데 이 미분을 계산하는 것은 입력에 가까운 층일 수록 힘들다. 왜냐하면 \(\bol..

1. 개요- 입력이 4개이며 출력은 3가지 클래스를 갖는 경우를 생각해보자. 신경망은 그림 1과 같다.- 입력과 파라미터를 아래와 같이 정의한다.$$\begin{eqnarray} x_n&=& \begin{bmatrix}x_{n1} & x_{n2} & x_{n3}& x_{n4} \end{bmatrix}, \quad w=\begin{bmatrix}w_{11} & w_{21} & w_{31} \\ w_{12} & w_{22} & w_{32} \\ w_{13} & w_{23} & w_{33} \\ w_{14} & w_{24} & w_{34} \end{bmatrix}, \quad b=\begin{bmatrix}b_{1} & b_{2} & b_{3} \end{bmatrix} \\ \\ u&=&\begin{bmatr..

1. 개요- 변수가 2개이며 종속변수가 이진형인 경우를 생각해보자. 신경망은 그림 1과 같다.- 훈련데이터의 수는 200으로 한다. - 출력이 이진형이므로 활성함수는 sigmoid로 한다. - 즉, \(u_1=w_{11}x_1+w_{12}x_2+b_1\)이며 \(z_1=f(u_1)=1/(1+exp(-u_1))\)이다. - \(x_1\)과 \(x_2\)는 \(U(-1,1)\)에서 각각 독립적으로 생성한다.- 출력 \(d\)는 아래와 같이 정의한다. 단, \(\varepsilon\)은 \(N(0, 0.3^2)\)를 따른다.\begin{eqnarray}d = \begin{cases} 1 & \text{if } x_2 > x_1 + 1 + \varepsilon \\ 0 & \text{otherwise} \end..