| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 전처리
- 역전파
- 딥러닝
- 오토인코더
- Python
- 합성곱 신경망
- CNN
- 베이지안
- A Neural Algorithm of Artistic Style
- SQL
- Gram matrix
- 수달
- c#
- Convolutional Neural Network
- bayesian
- 냥코 센세
- 신경망
- 비샤몬당
- Autoencoder
- 소수
- backpropagation
- 소인수분해
- 히토요시
- project euler
- 역전파법
- 자전거 여행
- 오일러 프로젝트
- mnist
- deep learning
- neural network
- Today
- Total
통계, IT, AI
딥러닝: 화풍을 모방하기 (6) - 연습: 다클래스 분류 문제 본문
1. 개요
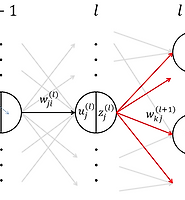
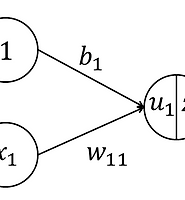
- 입력이 4개이며 출력은 3가지 클래스를 갖는 경우를 생각해보자. 신경망은 그림 1과 같다.

- 입력과 파라미터를 아래와 같이 정의한다.
-출력의 활성화 함수로 softmax 함수를 사용한다.
-오차함수로 교차엔트로피를 사용하자.
-
- 따라서 오차함수의 파라미터에 대한 미분을 다음과 같이 정의한다.
- 데이터는 Iris dataset을 사용한다. Iris dataset은 피셔가 제시한 다변수자료로 독립변수는 꽃받침의 길이, 꽃받침의 너비, 꽃잎의 길이 그리고 꽃잎의 너비이다. 종속변수는 꽃의 종류로 총 3가지로 분류가 있다. 자료의 수는 150개이며 해당 자료를 첨부한다. iris.csv
iris.csv
- 미니배치의 크기는 30, 반복횟수는 20000 그리고
2. 구현
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 | # -*- coding: utf-8 -*-import numpy as npimport matplotlib.pyplot as pltimport csvimport datetime as dt""" GENERAL SETTING """np.random.seed(0)enable_visualization = True""" DATA """with open('iris.csv', 'r') as f: dat = [row for row in csv.reader(f.readlines())] print('COLUMN: ', dat.pop(0)) temp_x, temp_d = [], [] for row in dat: temp_d.append(row.pop()) temp_x.append(row) X = np.asmatrix(temp_x, dtype=float) N, p = X.shape levels = list(set(temp_d)) K = len(levels) d = np.zeros((N, K), dtype=float) for row_num, level in enumerate(temp_d): d[row_num,levels.index(level)] = 1.0 print('N: ', N, ', p: ', p, ', K: ', K)""" FUNCTION """def activate(u_list): exp_u = np.exp(u_list) return np.diag((1/np.sum(exp_u, axis=1)).A1).dot(exp_u)def feedforward(X, w, b, activate_function=activate): X_ = np.column_stack((np.zeros(X.shape[0], dtype=float), X)) w_ = np.vstack((b, w)) return activate_function(X_.dot(w_))def error(X, w, b, d, feedforward_function=feedforward): return -np.sum(np.multiply(d, np.log(feedforward_function(X, w, b))))""" PARAMETER & OPTIMIZATION SETTING """w = np.zeros((p, K), dtype=float)b = np.zeros((1, K), dtype=float)epsilon = 0.001batch_size = 30epoch_size = 20000index_list = np.arange(N)np.random.shuffle(index_list)test_x = X[index_list[0:30],]test_d = d[index_list[0:30],]error_history = [error(test_x, w, b, test_d)]""" OPTIMIZATION """for epoch in range(epoch_size): np.random.shuffle(index_list) if epoch % 5000 == 0: print('epoch: ', epoch, ', ', dt.datetime.now()) for i in range(N//batch_size): selected_index_list = index_list[(i*batch_size):((i+1)*batch_size)] training_x, training_d = X[selected_index_list,], d[selected_index_list,] # Caculate nabla E der_w = training_x.T.dot(feedforward(training_x, w, b) - training_d)/batch_size der_b = np.mean(feedforward(training_x, w, b), axis=0) w -= epsilon * der_w b -= epsilon * der_b error_history.append(error(test_x, w, b, test_d))""" RESULT """print('w: ', w)print('b: ', b)if enable_visualization: plt.plot(error_history) plt.show()result = np.asmatrix(feedforward(X, w, b) > 0.5, dtype=float)error_rate = np.sum(np.array(result != d, dtype=int))//2.0 / Nprint(error_rate) |
3. 결과
- 전체 데이터에 대한 오분류율은 약 3%이며, 테스트 오차의 경향은 그림 2와 같다.

- 속도에 대한 이슈가 있다. 총 연산에 약 16초가 걸리는데 생각보다 느리다. 텐서플로우 사용을 고려하자.
- 지금까지는 파라미터의 초기값으로 0을 주었다. 하지만 언젠가 이 부분에 이슈가 있을 것이다.
- 학습률
- http://neuralnetworksanddeeplearning.com/에서 다음과 같은 내용을 보았다. 즉, classification을 진행할 때 출력층의 노드의 수가 왜 class의 수와 같아야 하는 것이다. 위의 예에서, 구분하고자 하는 꽃의 종류는 3가지이므로 이진수의 두개의 노드로도 충분하다. 첫번째 꽃은
- 하지만 이 방법은 성과가 그다지 좋지 않다. 왜냐하면 출력층의 각 원소가 무엇을 의미하는지 확실하지 않기 때문이다. 다른 예를 들면, 0부터 9까지의 숫자의 이미지가 있을 때 이를 분류하는 문제를 생각해보자. 이 경우
- 또한, 어째서 classfication의 에러 함수로 "오분류의 개수"로 하지 않는지에 대하여 보았다. 저자는 이에 대하여 신경망이 학습을 거듭해 가면서 개선되는 것을 연속형으로 나타내어 이전 학습과 비교하기 위함이라고 설명하였다.
'머신러닝' 카테고리의 다른 글
| 딥러닝: 화풍을 모방하기 (8) - 연습: 역전파법 (0) | 2017.03.01 |
|---|---|
| 딥러닝: 화풍을 모방하기 (7) - 책 요약: 4. 역전파법 (0) | 2017.02.16 |
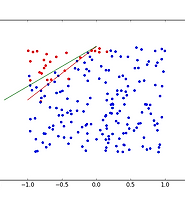
| 딥러닝: 화풍을 모방하기 (5) - 연습: 이진 분류 문제 (0) | 2017.02.01 |
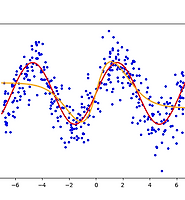
| 딥러닝: 화풍을 모방하기 (4) - 연습: 회귀 문제 (0) | 2017.01.30 |
| 딥러닝: 화풍을 모방하기 (3) - 책 요약: 3. 확률적 경사 하강법 (1) | 2017.01.30 |